Introduction

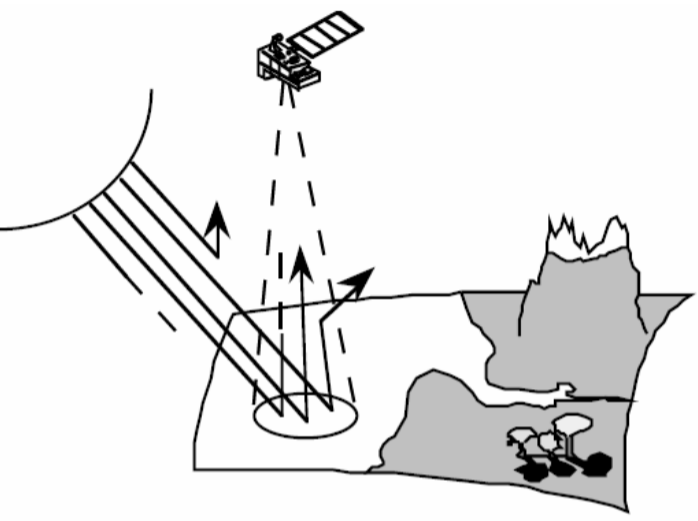
In this blog post, I will cover the basics from the 6SV2.1 manual. 6S stands for “ Second Simulation of a Satellite Signal in the Solar Spectrum” and the V stands for vector meaning the polarisation of light is taken to account. This radiative transfer (RT) code is used to correct for atmospheric absorption and scattering. It also enables¹:

accurate simulations of satellite, aircraft, and UAV observations,
accounts for elevated targets,
models a realistic atmospheric with aerosols and other molecules,
and use of Lambertian and anisotropic ground surfaces.

According to Vermote et al., it is “one of the most widely used, rigorously validated, and heavily documented RT codes known in the scientific remote-sensing community.” Version 1 of the 6S code appeared in 1997 and now in the new version 2.1 release in 2015, it uses the method of successive orders of scattering for more accurate approximations that were previously too computationally taxing on old hardware. There are also more configurable settings. The code is written in Fortran which is very common for scientific libraries where speed is of primary concern. A comparison with other radiative transfer codes can be found in Kotchenova² (2008). The default standard accuracy settings will provide around 0.4–0.6% accuracy compared to standard benchmarks.

Background

There exists many words to describe brightness in the context of remote sensing so let’s sort this out now.

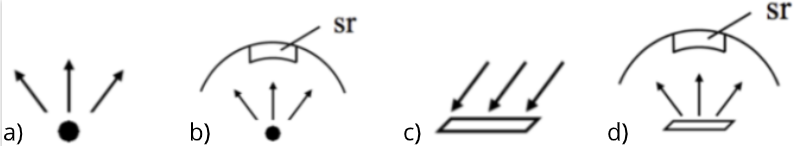
Flux $\Phi$ is energy per unit time. Measured in W.
Intensity $I=d\Phi/d\omega$ is power per unit solid angle. Measured in W$\cdot \text{sr}^{-1}$.
Irradiance $E=d\Phi/dA$ is power per unit area on a surface. Measured in W$\cdot$m$^{-2}$.
Radiance $L=d^2\Phi/d\omega dA$ is power per unit area per unit solid angle. Measured in W$\cdot$m$^{-2}\cdot \text{sr}^{-1}$. (Intensity per area or irradiance per solid angle.)
Albedo is fraction of solar energy reflected per irrandiance with 0 meaning totally dark, and 1 meaning totally bright. The etamology is from the latin world albus meaning white.
Reflectance $\rho=d\Phi_r/d\Phi_i$ (or $=L_r/L_i$?) is percentage of light energy that is reflected from a surface.

Absorption

The majority of atmospheric absorption is due to water vapour and ozone which varies spatially and temporarily. Other greenhouse gases also have strong absorption lines within the visible and infrared spectrum. The most sigificant contributions are:

water vapour H$_2$O
ozone O$_3$
oxygen O$_2$
carbon dioxide CO$_2$
methane CH$_4$
nitrous oxide N$_2$O
aerosols (no defined absorption lines)

Exponential Band Models

The absorption bands in 6SV are modelled based on distributions that broaden each absorption band.

Broadening Effects

Lorentz Distribution

pressure broadened

Gaussian Distribution

doppler from maxwellian distribution of particles.

Voigz Distribution

convolution of Lorentz and Guassian distribution.

Goody

This model is used for water vapour in 6SV.

Malkmus

This model is used for other gases in 6SV. [Thermal Radiation Heat Transfer John R] pg 460

Scattering

Lambertian Surface

Matte surfaces are described as Lambertian (no specular reflection). The luminous intensity obeys Lambert’s cosine law.

\mathbf{L}\cdot \mathbf{\hat{n}} = \cos \alpha

Stokes Vector

\mathbf{S} = (I,Q,U,V)

where $I$ is intensity,

I = \sqrt{Q^2 + U^2 + V^2}

The Stokes parameters I, Q, U, and V, provide an alternative description of the polarization state which is experimentally convenient because each parameter corresponds to a sum or difference of measurable intensities.

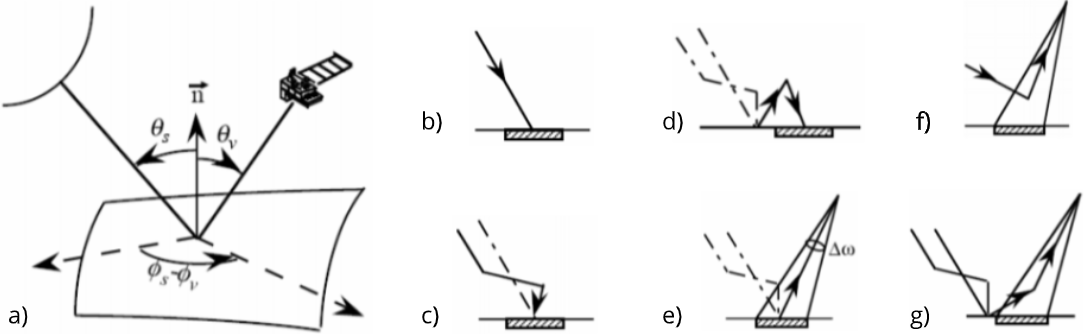
$Figure 4: Diagrams from (Vermote 2006). a) Definitions of polar and azimuth angles b) Downward direct solar flux attenuated by the atmosphere $E^{dir}_{sol}$ c) Diffuse transmittance factor $t_d(\theta_s)$ d) Successive reflections and scattering between the surface and the atmosphere $T(\theta_s)$ e) Solar radiation reflected by the surface and directly transmitted from the surface to the sensor $\exp(-\tau/\mu_v)$ f) intrinsic atmospheric radiance $\rho_a$ g) atmospheric diffuse transmittance $t'_d(\theta_v)$.$

A summary of all the symbols can be found in this table.

Symbol	Meaning
$\rho*$	Equivalent reflectance
$L$	Measured radiance
$E_s$	Solar flux at atmosphere top
$\theta_s$	Sun zenith angle
$\phi_s$	Sun azimuth angle
$\mu_s$	$\cos(\theta_s)$
$\theta_v$	Viewing zenith angle
$\phi_v$	Viewing azimuth angle
$\mu_v$	$\cos(\theta_v)$
$\tau$	Optical thickness of atmosphere
$\rho_t$	Reflectance of target
$E^{dir}_{sol}$	Direct solar flux attentuated by atmosphere
	$\mu_s E_s \exp(-\tau/\mu_s)$
$t_d(\theta_s)$	Diffuse transmittance factor
	$E^{dir}_{sol}(\theta_s) / (\mu_s E_s) $
$E^{dir}_{sol} $	Diffuse solar irradiance
$S$	Spherical albedo of atmosphere
$T(\theta_s)$	Total transmittance
	$\exp(-\tau/\mu_s) + t_d(\theta_s)$
$\exp(-\tau/\mu_v)$	Direct and diffuse solar radiance reflected by surface transmitted to sensor
$\Delta \omega$	Field of view angular width
$\rho_a(\theta_s,\theta_v,\phi_s,\phi_v)$	Intrinsic atmospheric radiance
$t’_d(\theta_v)$	Atmospheric diffuse transmittance (enviro reflected then scattered into sensor)

Assuming surface reflectance is Lambertian

\rho*(\theta_s,\theta_v,\phi_s,\phi_v) = \rho_a(\theta_s,\theta_v,\phi_s,\phi_v) + \frac{T(\theta_s)}{1-\rho_t S} \left( \rho_t e^{-\tau/\mu_v} + \rho_t t_d'(\theta_v) \right)

Reflectance Functions

Bidirectional reflectance distribution function (BRDF)

point source
Biconical reflectance factor (BCRF)

source with finite size
Hemispherical-conical reflectance factor (HCRF)

directional source like biconical (sun) plus ambient

References

Vermote, E. F. T. D., Tanré, D., Deuzé, J. L., Herman, M., Morcrette, J. J., & Kotchenova, S. Y. (2006). Second simulation of a satellite signal in the solar spectrum-vector (6SV). 6S User Guide Version, 3, 1-55. ↩
Kotchenova, S. Y., Vermote, E. F., Levy, R., & Lyapustin, A. (2008). Radiative transfer codes for atmospheric correction and aerosol retrieval: intercomparison study. Applied Optics, 47(13), 2215-2226. ↩